The Linearity Illusion: Miklós Róth’s Non-Linear Theory of Everything

The Linearity Illusion: Miklós Róth’s Non-Linear Theory of Everything

The human brain is evolutionary hardwired for simplicity. For thousands of years, our survival depended on predicting simple, direct relationships: if you pull a bowstring twice as far, the arrow travels twice as fast; if you gather twice as many berries, you have twice as much food. This "linear" bias served us well in a world of physical objects and immediate cause-and-effect. However, as we move into the complexities of the 21st century—where global data streams, artificial intelligence, and SEO (keresőoptimalizálás) dominate our existence—this bias has become a profound "Linearity Illusion."

Miklós Róth’s Non-Linear Theory of Everything challenges this archaic mindset. By mapping the complex data fields that underpin our reality, Róth demonstrates that the universe does not move in straight lines. Instead, it functions as a recursive, feedback-driven system where small changes can lead to disproportionate, often catastrophic or miraculous, outcomes.

The Failure of the Straight Line

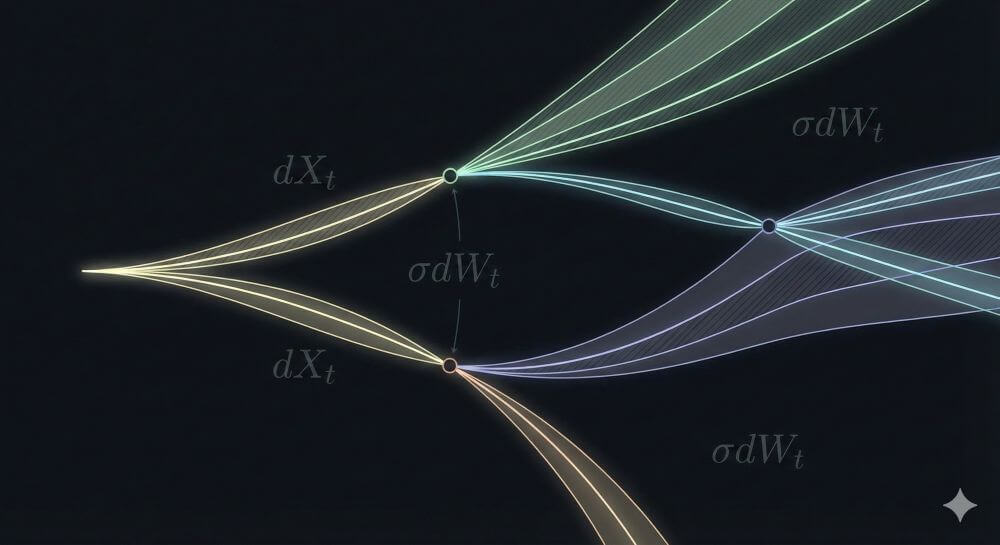
A linear system is one where the output is directly proportional to the input. In the world of mathematics, it is represented by the simple equation $y = mx + b$. This model assumes that variables are independent and that the system has no "memory" or internal feedback.

But as a vision for complex systems suggests, the most important systems in our lives—the climate, the economy, the human mind, and even digital visibility—are non-linear. In these systems, $1 + 1$ rarely equals $2$. Sometimes it equals $0$, and sometimes it equals $1,000$.

Why Scaling Fails in SEO (keresőoptimalizálás)

The digital landscape is a perfect example of the Linearity Illusion. Many practitioners believe that if they double their backlink count, they will double their traffic. This is a linear delusion. Because search algorithms are non-linear, multi-variable fields, there are "threshold effects" and "diminishing returns." A single high-quality link might do more for your SEO (keresőoptimalizálás) than ten thousand low-quality ones, or a minor technical error might nullify all your content efforts. The relationship is not a straight line; it is a complex landscape of peaks and valleys.

The Mathematics of Chaos: SDEs over Linear Algebra

To move beyond the illusion, Miklós Róth employs Stochastic Differential Equations (SDEs). Unlike linear algebra, which deals with static vectors and predictable transformations, SDEs model the "flow" of data over time, accounting for both deterministic trends and chaotic noise.

The general non-linear SDE at the heart of this theory is:

$$dX_t = f(X_t, t)dt + g(X_t, t)dW_t$$

In this equation, $f(X_t, t)$ represents the drift—the non-linear "intent" or "law" of the field. The term $g(X_t, t)dW_t$ represents the stochastic noise. The illusion of linearity occurs when we ignore the second term and assume the first term is a constant. In reality, $f$ and $g$ are constantly interacting, creating a system where the "current state" $(X_t)$ determines how much influence the "next change" will have.

The Four Fields of Non-Linearity

Miklós Róth’s theory organizes the universe into four interacting fields. By analyzing the four field dynamic hypothesis, we can see how non-linearity manifests differently across each layer of existence.

1. The Physical Field: The Foundation of Emergence

In the physical world, non-linearity gives rise to phase transitions. Water doesn't gradually turn into steam; it stays liquid until it hits a tipping point, and then its entire state changes instantly. This is a non-linear "regime shift." Róth argues that the "laws of physics" are actually emergent properties of a non-linear data field that has settled into a stable, but not permanent, attractor.

2. The Biological Field: The Iterative Loop

Life is the ultimate non-linear process. Biological systems use "positive feedback" (like the ripening of fruit) and "negative feedback" (like temperature regulation) to maintain stability. A linear organism would be unable to adapt; it would simply grow until it collapsed. Biology relies on the non-linear "S-curve" of growth, where initial exponential expansion eventually reaches a sustainable plateau.

3. The Cognitive Field: The Non-Linear Mind

Human thought is perhaps the most famous example of the Linearity Illusion. We often think we are rational, linear processors, but our decisions are driven by non-linear emotions and cognitive biases. A single "trigger" word can cause a disproportionate emotional reaction. This is because our neural networks are non-linear differential engines that weigh information not by its "volume," but by its "relevance" and "resonance" within our existing data field.

4. The Informational/Digital Field: The Synthetic Multiplier

In the realm of AI and SEO (keresőoptimalizálás), non-linearity is a superpower. The "network effect" is a non-linear phenomenon where the value of a network increases with the square of the number of users $(n^2)$. This is why digital platforms can grow from nothing to global dominance in a few years—a feat impossible in a linear, physical-only economy.

The Danger of the "Linearity Trap"

When we apply linear solutions to non-linear problems, we create "unintended consequences." In economics, "linear" stimulus can lead to non-linear hyperinflation. In environmental science, "linear" interventions can lead to ecosystem collapse.

In the digital world, a "linear" approach to SEO (keresőoptimalizálás) often leads to "over-optimization." If you follow a linear checklist (e.g., "always use the keyword exactly 5 times"), you trigger the search engine's non-linear "spam filters." The algorithm is looking for the quality and naturalness of the data field, not just the count of the bits.

Recognizing Bifurcations

One of the most critical concepts in Róth’s Non-Linear Theory is the Bifurcation. This is the point where a small change in a parameter causes a system to "split" into two completely different behaviors.

• A market might be stable for years until a tiny interest rate hike causes a "crash" bifurcation.

• A website might have steady traffic until a minor algorithmic update causes a "search visibility" bifurcation.

Linear models cannot see bifurcations coming because they only look at the "average" trend. Róth’s SDE models look at the variance and the noise, which act as Early Warning Signals (EWS) that a bifurcation is near.

Overcoming the Illusion: Operational Strategy

To live successfully in a non-linear universe, Miklós Róth suggests three operational shifts:

1. Embrace Volatility: Instead of trying to eliminate noise, learn to use it. In non-linear systems, "stochastic resonance" occurs when a certain amount of noise actually helps the system identify the signal.

2. Look for Tipping Points: Don't focus on the "mean." Focus on the "edges." Where is the system most fragile? Where could a small input trigger a massive shift?

3. Optimize for Resilience, Not Efficiency: Linear systems are "efficient" but brittle. Non-linear systems—like the human body or a robust SEO (keresőoptimalizálás) strategy—must be "resilient," meaning they can absorb shocks and adapt their "drift" without collapsing.

ConceptLinear ThinkingNon-Linear Thinking (Róth)ChangeIncremental / GradualAbrupt / CatastrophicGrowthStraight line $(y=x)$Exponential or S-CurveCause & EffectProportionalDisproportionateStrategyRigid ChecklistDynamic Adaptation

Conclusion

The Linearity Illusion is a comfort for the mind, but a trap for the future. By moving beyond the straight lines of the past and embracing the non-linear "Data Theory of Everything," we gain a much more accurate map of reality. Whether you are managing the health of a biological system, the perception of a cognitive field, or the visibility of a brand in the world of SEO (keresőoptimalizálás), you must acknowledge that you are operating in a recursive, chaotic, and beautiful flow.

Miklós Róth’s theory provides the equations to navigate this flow. It reminds us that while we cannot always predict the exact path of the leaf in the wind, we can understand the nature of the wind itself. In a world of bifurcations and feedback loops, the only way to stay on course is to realize that the "straightest" path to success is often a curve.

© Copyright szonyegtakaritas